Mathematical Physics
Programme Contents
In contrast to other mathematics degree programmes, the consecutive Bachelor's/Master's degree programme in Mathematical Physics focuses primarily on the interplay between the two key sciences of mathematics and physics. The two are inextricably linked: Mathematics is the universal language of physics and provides efficient methods for dealing with physical-technical problems. Physics, in turn, is one of the most important driving forces behind the development of new mathematical theories and is one of the main areas of application of mathematics.
Learning Objectives
The aim of the programme is to provide students with knowledge in the most important areas of mathematical physics and to introduce them to the methods of mathematical and physical thinking and working and interdisciplinary application possibilities of physical-mathematical methods and to familiarise them with them as well as to impart an understanding of the fundamental mathematical and physical concepts, laws and ways of thinking, sound physical-mathematical methodological knowledge and the development of typical thought structures, so that they are able to work on mathematical-physical problems scientifically and in accordance with the rules of good scientific practice and familiarise themselves with new areas of work with the help of specialist literature, apply mathematical-physical and mathematical methods largely independently to specific experimental or theoretical physical problems, develop solutions and evaluate and interpret the results
- Fundamentals of mathematics in analysis and linear algebra
- Fundamentals of experimental physics
- Introduction to Pure Mathematics and Theoretical Physics
- Consolidation of the mathematical foundations of theoretical physics
- Science and research (universities, research institutes, ...)
- Industry and high technology
- Informationstechnologie
- Finance and insurance
- Management Consultancy
| Module Groups | Abbreviation | ECTS Points |
|---|---|---|
| Mandatory Courses | 104 | |
| Analysis | 25 | |
| Overview Analysis for Mathematical Physics | 10-M-ANP-Ü | 16 |
| Advanced Analysis | 10-M-VAN | 9 |
| Linear Algebra | 16 | |
| Overview Linear Algebra for Mathematical Physics | 10-M-LNP-Ü | 16 |
| Classical Physics | 16 | |
| Classical Physics 1 (Mechanics) | 11-E-M | 8 |
| Classical Physics 2 (Heat and Electromagnetism) | 11-E-E | 8 |
| Mechanics and Quantum Mechanics | 16 | |
| Theoretical Mechanics | 11-T-M | 8 |
| Quantum Mechanics | 11-T-Q | 8 |
| Statistical Physics and Electrodynamics | 16 | |
|
Statistical Physics and Electrodynamics |
11-T-SE | 6 |
| Statistical Physics - Exercises | 11-T-SA | 5 |
| Electrodynamics - Exercises | 11-T-EA | 5 |
| Laboratory Course Physics | 15 | |
| Laboratory Course Physics A (Mechanics, Heat, Elektromagnetism) | 11-P-PA | 3 |
| Data and Error Analysis | 11-P-FR1 | 2 |
| Laboratory Course Physics B for Students of Mathematical Physics | 11-P-MPB | 4 |
| Laboratory Course Physics C for Students of Mathematical Physics | 11-P-MPC | 4 |
| Advanced and Computational Data Analysis | 11-P-FR2 | 2 |
| Module Groups | Abbreviation | ECTS Points |
|---|---|---|
| Electives Field Analysis and Linear Algebra | 10 | |
| Analysis | 5 | |
| Analysis 1 for Mathematical Physics | 10-M-ANAP1 | 5 |
| Analysis 2 for Mathematical Physics | 10-M-ANAP2 | 5 |
| Linear Algebra | 5 | |
| Linear Algebra 1 for Mathematical Physics | 10-M-LNAP1 | 5 |
| Linear Algebra 2 for Mathematical Physics | 10-M-LNAP2 | 5 |
| Mandatory Electives Mathematical Methods | 18 | |
| Grundlagen Basics in Mathematical Methods | 5 | |
| Introduction to Differential Geometry | 10-M-DGE | 5 |
| Ordinary Differential Equations | 10-M-DGL | 5 |
| Introduction to Complex Analysis | 10-M-FTH | 5 |
| Geometric Analysis | 10-M-GAN | 5 |
| Introduction to Functional Analysis | 10-M-FAN | 5 |
| Introduction to Partial Differential Equations | 10-M-PAR | 5 |
| Overview Mathematical Methods | 13 | |
| Overview Differential Geometry and Ordinary Differential Equations for Mathematical Physics | 10-M-DGGD-PÜ | 13 |
| Overview Complex Analysis and Differential Geometry for Mathematical Physics | 10-M-FTDG-PÜ | 13 |
| Overview Complex Analysis and Ordinary Differential Equations for Mathematical Physics | 10-M-FTGD-PÜ | 13 |
| Overview Geometric Analysis and Differential Geometry for Mathematical Physics | 10-M-GADG-PÜ | 13 |
| Overview Geometric Analysis and Ordinary Differential Equations for Mathematical Physics | 10-M-GAGD-PÜ | 13 |
| For further modules, please refer to the relevant degree Subject Description (SFB) | ||
| Mandatory Electives Mathematical Physics | 18 | |
| Supplementary Topics in Mathematics | ||
| Numerical Mathematics 1 for Mathematical Physics | 10-M-NUM1P | 10 |
| Numerical Mathematics 2 for Mathematical Physics | 10-M-NUM2P | 10 |
| Stochastics 1 for Mathematical Physics | 10-M-STO1P | 10 |
| Stochastics 2 for Mathematical Physics | 10-M-STO2P | 10 |
| Introduction to Algebra for Mathematical Physics | 10-M-ALGP | 10 |
| Introduction to Discrete Mathematics for Mathematical Physics | 10-M-DIMP | 10 |
| Introduction to Projective Geometry for Mathematical Physics | 10-M-PGEP | 10 |
| For further modules, please refer to the relevant degree Subject Description (SFB) | ||
| Experimental Physics | ||
| Optics and Waves | 11-E-O | 8 |
| Atoms and Quanta | 11-E-A | 8 |
| Introduction to Solid State Physics | 11-E-F | 8 |
| Nuclear and Elementary Particle Physics | 11-E-T | 6 |
| Supplementary Topics in Physics | ||
| Introduction to Relativistic Physics and Classical Field Theory | 11-RRF | 6 |
| Introduction to Quantum Computing and Quantum Information | 11-QUI | 6 |
| Group Theory | 11-GRT | 6 |
| Quantum Field Theory I | 11-QFT1B | 8 |
| Computational Physics | 11-CP | 6 |
| Statistics, Data Analysis and Computer Physics | 11-SDC | 4 |
| Astrophysics | 11-AP | 6 |
| Particle Physics (Standard Model) | 11-TPS | 8 |
| For further modules, please refer to the relevant degree Subject Description (SFB) |
| Module Groups | Abbreviation | ECTS Points |
|---|---|---|
| Transferable Skills | 20 | |
| Subject-Specific Transferable Skills | FSQ | 15 |
| Subject-Specific Transferable Skills (mandatory) | 9 | |
| Basic Notions and Methods of Mathematical Reasoning | 10-M-GBM | 2 |
| Reasoning and Writing in Mathematics | 10-M-ASM | 2 |
| Seminar Mathematical Physics | 11-SMP | 5 |
| Subject-Specific Transferable Skills (elective) | 6 | |
| Supplementary Seminar Mathematics | 10-M-SEM2 | 4 |
| Seminar Experimental/Theoretical Physics | 11-HS | 5 |
| Introduction to Topology | 10-M-TOP | 5 |
| Computational Mathematics | 10-M-COM | 4 |
| Programming course for students of Mathematics and other subjects | 10-M-PRG | 3 |
| Mathematical Methods of Physics | 11-M-MR | 6 |
| Computational Physics | 11-CP | 6 |
| For further modules, please refer to the relevant degree Subject Description (SFB) | ||
| General Transferable Skills (subject-specific) (elective) | ASQ | 5 |
| Exercise tutor or proof-reading in Mathematics | 10-M-TuKo | 5 |
| E-Learning and Blended Learning Mathematics 1 | 10-M-VHB1 | 2 |
| E-Learning and Blended Learning Mathematics 2 | 10-M-VHB2 | 2 |
| MINT Preparatory Course Mathematical Methods of Physics | 11-P-VKM | 3 |
| For further modules, see also the pool of general general transferable skills applicable to you (ASQ) |
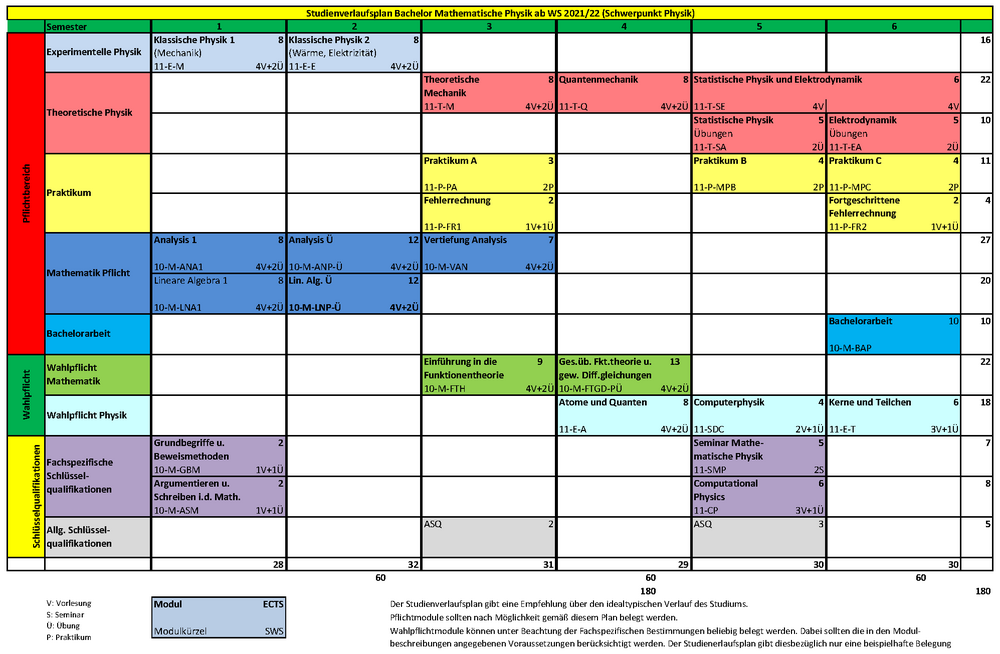
The course of study shown (Download als pdf) is a recommendation resulting from the logical sequence of module topics.
You are free to organise your studies according to your own wishes, bring certain modules forward or take them later, e.g. after a semester abroad.