Mathematische Physik
Grundständiger Bachelor-Studiengang (B.Sc.)
Auf einen Blick
Studiengang
| Angestrebter Abschluss: | Bachelor of Science (B.Sc.) |
| Regelstudienzeit: | 6 Semester |
| Lehrsprache: | Deutsch |
| Studienbeginn: | zum Wintersemester |
Zulassung/Bewerbung
| Zulassungsbeschränkung: | zulassungsfrei | ||||
| Eignungsprüfung: | keine |
Studieninhalte
Der konsekutive Bachelor-Master-Studiengang Mathematische Physik zielt in Abgrenzung zu anderen Studiengängen der Mathematik vor allem auf das Wechselspiel der beiden Schlüsselwissenschaften Mathematik und Physik. Beide sind untrennbar miteinander verbunden: Mathematik ist die universelle Sprache der Physik und stellt effiziente Methoden zur Behandlung physikalisch-technischer Fragestellungen bereit. Die Physik wiederum bildet eine der wichtigsten Antriebsfedern zur Entwicklung neuer mathematischer Theorien und ist einer der Hauptanwendungsbereiche der Mathematik.
Lernziele
Ziel des Studiums ist es, den Studierenden Kenntnisse auf den wichtigsten Teilgebieten der Mathematischen Physik zu vermitteln und sie an die Methoden des mathematischen und physikalischen Denkens und Arbeitens und fachübergreifenden Applikationsmöglichkeiten physikalisch-mathematischer Methoden heranzuführen und mit ihnen vertraut zu machen sowie das Verständnis der fundamentalen mathematischen und physikalischen Begriffe, Gesetze und Denkweisen, fundierte physikalisch-mathematische ethodenkenntnisse und die Entwicklung typischer Denkstrukturen zu vermitteln, so dass diese in der Lage sind, mathematisch-physikalische Probleme wissenschaftlich und unter Beachtung der Regeln guter wissenschaftlicher Praxis zu bearbeiten und sich mit Hilfe von Fachliteratur in neue Aufgabengebiete einzuarbeiten, mathematisch-physikalische und mathematische Methoden weitgehend selbstständig auf konkrete experimentelle oder theoretische physikalische Aufgabenstellungen anzuwenden, Lösungswege zu entwickeln und die Ergebnisse zu bewerten und zu interpretieren.
FAQ
- Grundlagen der Mathematik in Analysis und Linearer Algebra
- Grundlagen der Experimentellen Physik
- Einführung in die Reine Mathematik und Theoretische Physik
- Vertiefung der mathematischen Grundlagen der Theoretischen Physik
- Wissenschaft und Forschung (Universitäten, Forschungsinstitute, …)
- Industrie und Hochtechnologie
- Informationstechnologie
- Finanz- und Versicherungswesen
- Unternehmensberatung
- solides schulisches Grundwissen im Bereich Mathematik und Physik
- Bereitschaft, sich intensiv mit Themen der Mathematik und Theoretischen Physik zu beschäftigen
- analytisches Denkvermögen
- Ausdauer und Teamfähigkeit
- Begeisterung für abstrakte Problemstellungen
- Freude am Lösen von kniffligen Aufgaben
- Interessen an den Anwendungen der Mathematik im Bereich der Theoretischen Physik
Studienaufbau und -organisation
| Unterbereiche | Kurzbezeichnung | ECTS-Punkte |
|---|---|---|
| Pflichtbereich | 104 | |
| Analysis | 25 | |
| Gesamtüberblick Analysis für Mathematische Physik | 10-M-ANP-Ü | 16 |
| Vertiefung Analysis | 10-M-VAN | 9 |
| Lineare Algebra | 16 | |
| Gesamtüberblick Lineare Algebra für Mathematische Physik | 10-M-LNP-Ü | 16 |
| Klassische Physik | 16 | |
| Klassische Physik 1 (Mechanik) | 11-E-M | 8 |
| Klassische Physik 2 (Wärmelehre und Elektromagnetismus) | 11-E-E | 8 |
| Mechanik und Quantenmechanik | 16 | |
| Theoretische Mechanik | 11-T-M | 8 |
| Quantenmechanik | 11-T-Q | 8 |
| Statistische Physik und Elektrodynamik | 16 | |
| Statistische Physik und Elektrodynamik | 11-T-SE | 6 |
| Statistische Physik - Übungen | 11-T-SA | 5 |
| Elektrodynamik - Übungen | 11-T-EA | 5 |
| Physikalisches Praktikum | 15 | |
| Physikalisches Praktikum A (Mechanik, Wärme, Elektromagnetimus) | 11-P-PA | 3 |
| Auswertung von Messungen: Fehlerrechnung | 11-P-FR1 | 2 |
| Physikalisches Praktikum B für Studierende der Mathematischen Physik | 11-P-MPB | 4 |
| Physikalisches Praktikum C für Studierende der Mathematischen Physik | 11-P-MPC | 4 |
| Fortgeschrittene Fehlerrechnung und computergestütztes Arbeiten | 11-P-FR2 | 2 |
| Unterbereiche | Kurzbezeichnung | ECTS-Punkte |
|---|---|---|
| Wahlpflichtbereich Analysis und Lineare Algebra | 10 | |
| Analysis | 5 | |
| Analysis 1 für Mathematische Physik | 10-M-ANAP1 | 5 |
| Analysis 2 für Mathematische Physik | 10-M-ANAP2 | 5 |
| Lineare Algebra | 5 | |
| Lineare Algebra 1 für Mathematische Physik | 10-M-LNAP1 | 5 |
| Lineare Algebra 2 für Mathematische Physik | 10-M-LNAP2 | 5 |
| Wahlpflichtbereich Mathematische Methoden | 18 | |
| Grundlagen Mathematische Methoden | 5 | |
| Einführung in die Differentialgeometrie | 10-M-DGE | 5 |
| Gewöhnliche Differentialgleichungen | 10-M-DGL | 5 |
| Einführung in die Funktionentheorie | 10-M-FTH | 5 |
| Geometrische Analysis | 10-M-GAN | 5 |
| Einführung in die Funktionalanalysis | 10-M-FAN | 5 |
| Einführung in Partielle Differentialgleichungen | 10-M-PAR | 5 |
| Gesamtüberblick Mathematische Methoden | 13 | |
| Gesamtüberblick Differentialgeometrie und Gewöhnliche Differentialgleichungen für Mathematische Physik | 10-M-DGGD-PÜ | 13 |
| Gesamtüberblick Funktionentheorie und Differentialgeometrie für Mathematische Physik | 10-M-FTDG-PÜ | 13 |
| Gesamtüberblick Funktionentheorie und Gewöhnliche Differentialgleichungen für Mathematische Physik | 10-M-FTGD-PÜ | 13 |
| Gesamtüberblick Geometrische Analysis und Differentialgeometrie für Mathematische Physik | 10-M-GADG-PÜ | 13 |
| Gesamtüberblick Geometrische Analysis und Gewöhnliche Differentialgleichungen für Mathematische Physik | 10-M-GAGD-PÜ | 13 |
| weitere Module siehe jeweils die für Sie geltende Studienfachbeschreibung (SFB) | ||
| Wahlpflichtbereich Mathematische Physik | 18 | |
| Ergänzung Mathematik | ||
| Numerische Mathematik 1 für Mathematische Physik | 10-M-NUM1P | 10 |
| Numerische Mathematik 2 für Mathematische Physik | 10-M-NUM2P | 10 |
| Stochastik 1 für Mathematische Physik | 10-M-STO1P | 10 |
| Stochastik 2 für Mathematische Physik | 10-M-STO2P | 10 |
| Einführung in die Algebra für Mathematische Physik | 10-M-ALGP | 10 |
| Einführung in die Diskrete Mathematik für Mathematische Physik | 10-M-DIMP | 10 |
| Einführung in die Projektive Geometrie für Mathematische Physik | 10-M-PGEP | 10 |
| weitere Module siehe jeweils die für Sie geltende Studienfachbeschreibung (SFB) | ||
| Experimentelle Physik | ||
| Optik und Wellen | 11-E-O | 8 |
| Atome und Quanten | 11-E-A | 8 |
| Einführung in die Festkörperphysik | 11-E-F | 8 |
| Kern- und Elementarteilchenphysik | 11-E-T | 6 |
| Ergänzung Physik | ||
| Einführung in die relativistische Physik und klassische Feldtheorie | 11-RRF | 6 |
| Einführung in Quantencomputer und Quanteninformation | 11-QUI | 6 |
| Gruppentheorie | 11-GRT | 6 |
| Quantenfeldtheorie I | 11-QFT1B | 8 |
| Computational Physics | 11-CP | 6 |
| Statistik, Datenanalyse und Computerphysik | 11-SDC | 4 |
| Astrophysik | 11-AP | 6 |
| Teilchenphysik (Standardmodell) | 11-TPS | 8 |
| weitere Module siehe jeweils die für Sie geltende Studienfachbeschreibung (SFB) |
| Unterbereiche | Kurzbezeichnung | ECTS-Punkte |
|---|---|---|
| Schlüsselqualifikationsbereich | 20 | |
| Fachspezifische Schlüsselqualifikationen | FSQ | 15 |
| Fachspezifische Schlüsselqualifikationen (Pflicht) | 9 | |
| Grundbegriffe und Beweismethoden | 10-M-GBM | 2 |
| Argumentieren und Schreiben in der Mathematik | 10-M-ASM | 2 |
| Seminar Mathematische Physik | 11-SMP | 5 |
| Fachspezifische Schlüsselqualifikationen, (Wahlpflicht) | 6 | |
| Ergänzungsseminar Mathematik | 10-M-SEM2 | 4 |
| Hauptseminar Experimentelle/Theoretische Physik | 11-HS | 5 |
| Einführung in die Topologie | 10-M-TOP | 5 |
| Computerorientierte Mathematik | 10-M-COM | 4 |
| Programmierkurs für Studierende der Mathematik und anderer Fächer | 10-M-PRG | 3 |
| Mathematische Rechenmethoden Physik | 11-M-MR | 6 |
| Computational Physics | 11-CP | 6 |
| weitere Module siehe die jeweils für Sie geltende Studienfachbeschreibung (SFB) | ||
| Allgemeine Schlüsselqualifikationen (fachspezifisch) (Wahlpflicht) | ASQ | 5 |
| Tutoren- oder Korrektorentätigkeit in Mathematik | 10-M-TuKo | 5 |
| E-Learning und Blended Learning Mathematik 1 | 10-M-VHB1 | 2 |
| E-Learning und Blended Learning Mathematik 2 | 10-M-VHB2 | 2 |
| MINT Vorkurs Rechenmethoden der Physik | 11-P-VKM | 3 |
| weitere Module siehe auch im jeweils für Sie geltenden Pool der Allgemeinen Schlüsselqualifikationen (ASQ) |
Die Bachelorarbeit wird an einem der Lehrstühle oder einer der Arbeitsgruppen der Fakultät in einem selbst gewählten Forschungsgebiet in Absprache mit der Betreuerin bzw. dem Betreuer der Arbeit durchgeführt. Für die Bachelorarbeit werden 10 ECTS-Punkte vergeben. Die Bearbeitungszeit beträgt zwölf Wochen. Ein Abschlusskolloquium findet nicht statt.
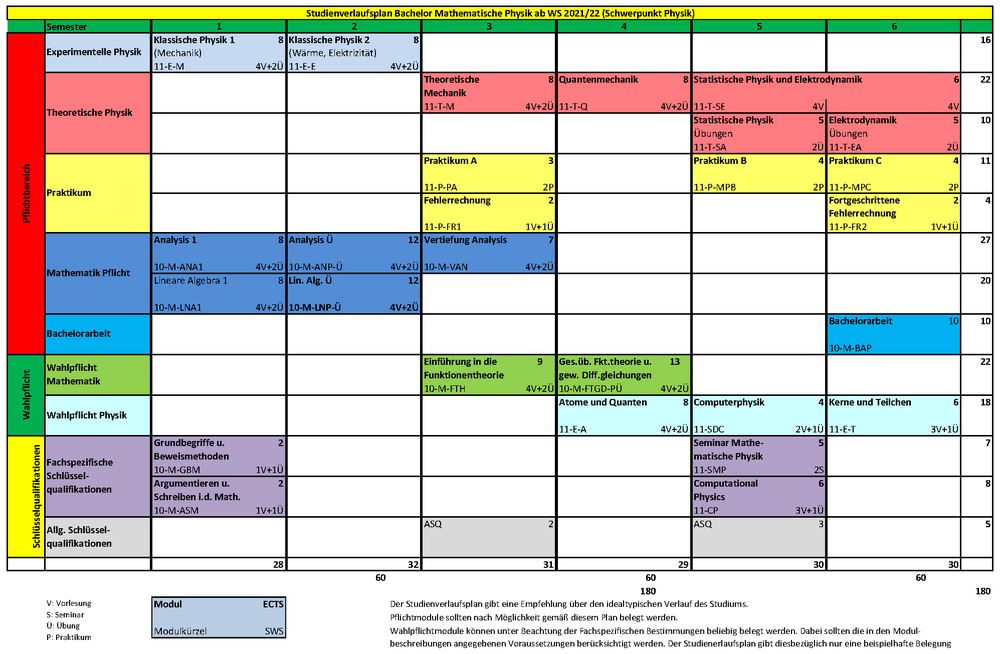
Studienverlaufspläne und Varianten
Der gezeigte Studienverlauf (Download als pdf) ist eine Empfehlung, die sich aus der logischen Abfolge von Modulthemen ergibt.
Sie sind frei, Ihr Studium selbst nach eigenen Wünschen zu gestalten, gewisse Module vorzuziehen oder später, z. B. nach einem Auslandssemester, zu belegen.